Polycube

A polycube puzzle is a puzzle like the Soma cube, or like the one pictured below.

Polycube puzzle

In summer or fall of 2019, I wrote a program to solve polycube puzzles. I did this so I could design and 3D print my own puzzle (which is the puzzle above).

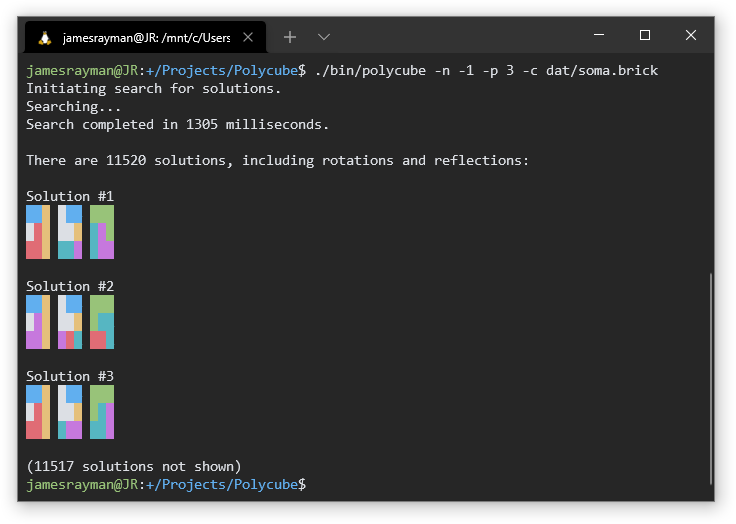
Polycube solver demo

The solver works by generating all possible translations and rotations of each polycube, and then translating that into an exact cover problem. The exact cover problem is NP-hard1, so making a state-of-the-art solver is quite a challenge. The exact cover solver I implemented by myself is good enough for simple polycube puzzles like the two above, but I could probably make it much faster by reducing the problem to 3SAT and using a SAT solver library.

I want a faster solver so I can design a puzzle bag: a bag of 29 polycubes from which you randomly pick 20 to assemble into a cube. Compared to a single puzzle, a puzzle bag is more interesting to solve multiple times since you pick a new combination of polycubes every time. A puzzle bag could also be used for competitive solving: in a single round, all competitors are given the same set of 20 polycubes to solve, much like how in Rubik’s Cube competitions all competitors are given the same scramble. Of course, every combination of polycubes from the bag should result in a solvable puzzle, which is why I want to make my solver faster. It’ll take 200 days of CPU time to verify the bag with the solver that I have now2.

  1. This solution method does not prove that polycube packing is NP-hard. Polycube packing is NP-hard, though, since 3SAT can be reduced to it. ↩

  2. 200 days isn’t that much compared to the almost 2 years since I’ve put down the project. But, figuring out how to speed up the solver sounds a lot more fun that monitoring the solver for an extended period of time. ↩


13 July 2021